Gabriel Peyré

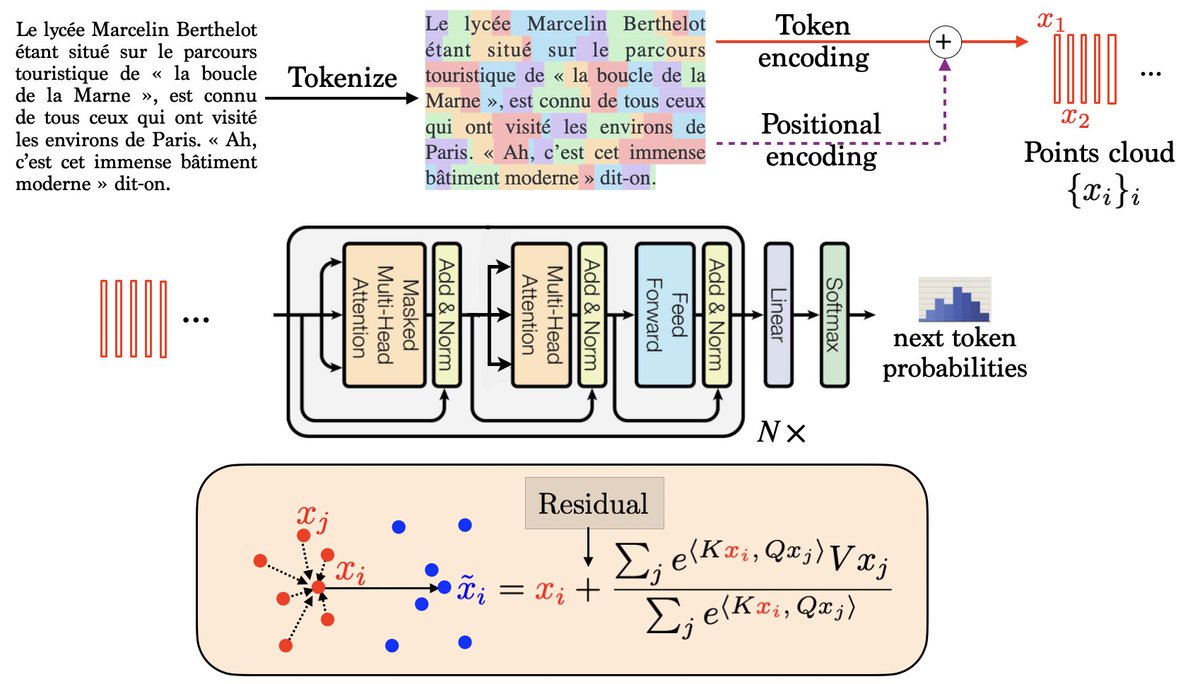
"Transformers are Universal In-context Learners": in this paper, we show that deep transformers with a fixed embedding dimension are universal approximators for an arbitrarily large number of tokens. arxiv.org/abs/2408.01367

Oldies but goldies: A. Brandt, Multi-Level Adaptive Solutions to Boundary-Value Problems, 1977. Introduces the multigrid method, which is the fundamental tool to speed up the convergence of low frequencies for the resolution of PDEs. en.wikipedia.org/wiki/Multigrid…

Nonlinearity matters. Linear diffusion (heat) has non-compactly supported solutions. Non-linear diffusion (porous medium) drives dynamics with compactly supported solutions. The porous medium is the simplest case, studied in detail by Otto. mis.mpg.de/preprints/1999…

Oldies but goldies: M Eck, T DeRose, T Duchamp, H Hoppe, M Lounsbery, W Stuetzle, Multiresolution analysis of arbitrary meshes, 1995. hhoppe.com/proj/mra/

Optimization algorithms come with many flavors depending on the structure of the problem. Smooth vs non-smooth, convex vs non-convex, stochastic vs deterministic, etc. en.wikipedia.org/wiki/Mathemati…

Oldies but goldies: J. B. Kruskal, On the shortest spanning subtree of a graph and the traveling salesman problem, 1956. Computes the minimum spanning tree in n*log(n) operations. en.wikipedia.org/wiki/Prim%27s_…

The Laplacian pyramid is the ancestor of the wavelet transform. Defines a compact multiscale representation by iterative lowpass/highpass filterings. en.wikipedia.org/wiki/Pyramid_(…

Oldies but goldies: J Koenderink, The structure of images, 1984. Introduces (with A. Witkin) the notion of scale space, i.e., the multi-scale analysis of signals and images, which is at the heart of many vision architectures. en.wikipedia.org/wiki/Scale_spa…

Oldies but goldies: D Hubel, T Wiesel, Receptive fields, binocular interaction and functional architecture in the cat's visual cortex, 1962. Describes the organisation of the visual cortex using oriented filters. Nobel prize in 1981. youtube.com/watch?v=IOHayh…

Cats, bunnies, and elephants in graphics and applied maths.

Oldies but goldies: R.L. Harder and R.N. Desmarais, Interpolation using surface splines, 1972. Thin plate (biharmonic) splines is a popular interpolation method with a closed form thanks to the theory of reproducing Hilbert spaces. Defines a Sobolev space of smooth functions.…

The solution of the Eikonal equation is solved by advancing a front in the normal direction, similar to a grass fire. The most famous Hamilton-Jacobi equation. Refraction occurs when the speed has a discontinuity (Snell-Descart)

Oldies but goldies: T Gonzalez, Clustering to minimize the maximum intercluster distance, 1985. Popularized the farthest point sampling greedy algorithm. en.wikipedia.org/wiki/Farthest-…

Reaction-diffusion with spatially varying weights. en.wikipedia.org/wiki/Reaction%… fr.wikipedia.org/wiki/The_Chemi…

Oldies but goldies: J Blinn, A Generalization of Algebraic Surface Drawing, 1982. "Metaballs" are levelsets of mixtures of radial basis functions, which generate blobby lava-lamp-like behaviors. en.wikipedia.org/wiki/Metaballs

Birkhoff's contraction for Hilbert's metric is a key tool to quantify convergence of Markov-Chains (Perron-Frobenius). en.wikipedia.org/wiki/Hilbert_m…

Oldies but goldies: D Immel, M Cohen, D Greenberg, A radiosity method for non-diffuse environments, 1986. Describes conservation of light as an integral equation which is at the heart of global rendering techniques such as radiosity. en.wikipedia.org/wiki/Rendering…

Wave equation on a surface. en.wikipedia.org/wiki/Wave_equa…

Oldies but goldies: J. Bertrand, Theoreme relatif au mouvement d'un point attire vers un centre fixe, 1873. Only harmonic spring and gravity central forces produce periodic motions. en.wikipedia.org/wiki/Bertrand%…

Multilayer perceptron with 1 hidden layer breaks the curse of dimensionality for Barron's functions. stat.yale.edu/~arb4/publicat…

Oldies but goldies: A. J. Lotka, Contribution to the Theory of Periodic Reaction, 1910. Lotka-Volterra is a non-linear ODE modeling chemical reaction or prey/predator behaviors which exhibits periodic solutions. en.wikipedia.org/wiki/Lotka%E2%…