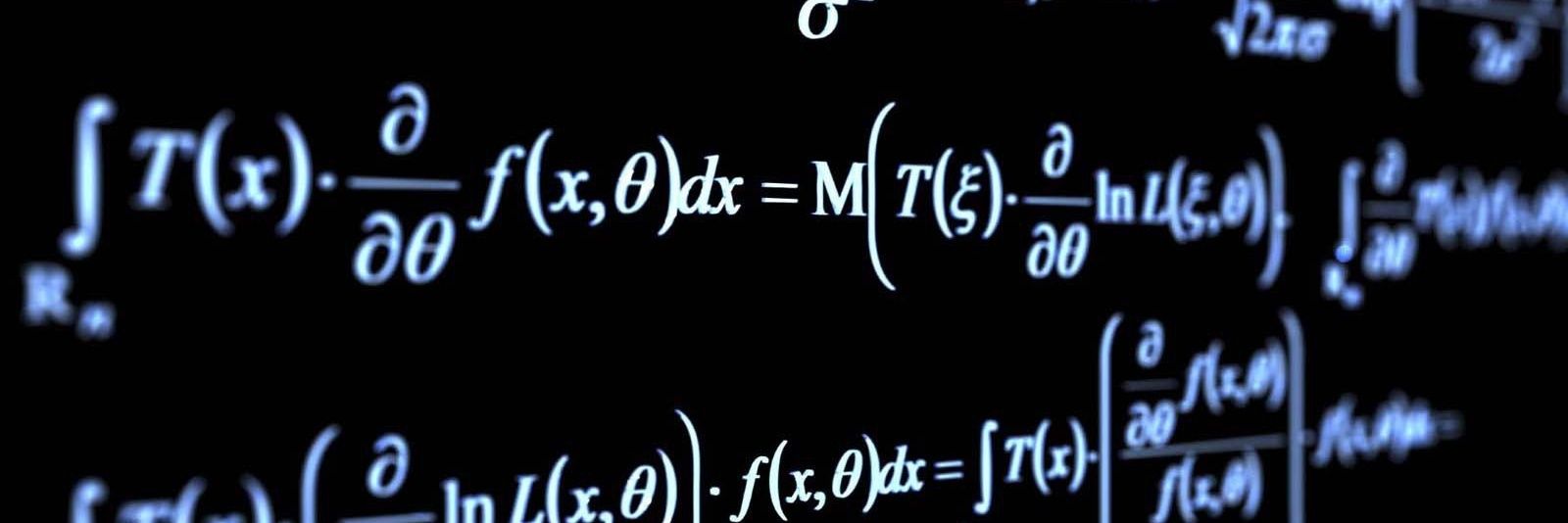
Quadratica
@Quadratica87928
You will find it when you are not looking.
👉"Leibniz' Rule" with constant upper & lower integral limits also known as 💡"Feynman's Integral Trick": Compute the following integrals using this trick and show your results: (Note I₁₁ can also be calculated by complex/contour integration, ☝️"Cauchy's Residue Thm"):
Entropy is often said to be the disorder of a system, as it is determined by the number of random microstates. A microstate is a microscopic configuration consistent with the macroscopic quantities that characterize a thermodynamic system. #MathType #math #mathfacts
Maryam Mirzakhani was the first woman to win a Fields Medal, and made key contributions to the fields of hyperbolic geometry and Riemann surfaces. #MathType #math #mathematics #mathematical #mathematician #mathproblems #mathfacts
A page from Srinivasa Ramanujan's notebooks, penned by him during 1903-1910, used to demonstrate his mathematical prowess to potential benefactors.
Johannes Diderik van der Waals, born #OnThisDay in 1837, was a prominent Dutch physicist renowned for his groundbreaking work in the understanding of the properties of gases and liquids. His most notable contribution is the Van der Waals equation of state, which improved upon the…
Computing the Maximum Likelihood Estimator (MLE) for Poisson Distribution.
Markov's inequality is one of the basic results in probability, which relates probabilities to expectations, and provides bounds for the cumulative distribution function of a #random variable. #MathType #math #mathematics #mathematical #mathematician #mathproblems #mathfacts
Schrödinger equation can predict the wave function (state) of a system and its evolution in time. It's Newton's law analog for #QuantumMechanics #MathType #math #mathematics #mathematical #mathematician #mathproblems #mathfacts
Cyclotomic polynomials are polynomials whose complex roots are primitive roots of unity. They play an important role in algebraic #NumberTheory and #Galois theory, being used to build abelian field extensions. #MathType #math #mathematics #mathematical #mathproblems #mathfacts
On computing expectations of functions of Poisson random variables by using infinite series expansions.
Problem: Suppose that the joint PDF of (X,Y) is given by: f(x,y)=0.5y²e⁻ˣ, 0<y<x<∞; and 0, otherwise. Find the value of ℙ(Y<1|X=3).
Here's my attempt at a number systems visual. I decided to leave off Imaginary (you just multiply something by i) and Complex (you just add Imaginary to non-Imaginary). Letters and numbers just get too small to be useful. @pickover
#POTD #Math #Calculus #Integration Problem of the Day! Here's the last integral before the one I post Friday. It's another one you could integrate directly, though it would be a hassle.
The Standard Model Lagrangian provides a unified description of 3 of the 4 fundamental forces in Nature: - electromagnetic - weak force - strong force Physicists were able to predict the properties of particles before they were experimentally discovered, ex Higgs boson
A mean field evolution is the large number limit of particles systems. The simplest case is gradient descent, which corresponds to an advection equation in the limit. en.wikipedia.org/wiki/Advection en.wikipedia.org/wiki/Mean_fiel…
Laplace transform converts a function that depends on a real variable t into a function that depends on a complex variable s. This mathematical tool finds widespread application in engineering, particularly in circuit analysis. #MathType #math #mathematics #mathfacts